月別アーカイブ: 2010年3月

【儲かる工場の作り方】第十二話「ゼロエミッション」

Title12
動脈産業・静脈産業

モノ造りをすれば、多かれ少なかれ環境に影響を与えることになる。与えた影響を浄化しなければならない。生態系を人体に例えれば、モノ造りは動脈。市場に製品（酸素）を供給し、活動エネルギーとする。廃棄物（二酸化炭素）を回収するのが静脈だ。
これからの産業は動脈と静脈を併せ持っていなければならない。リデュース（削減）リユース（再利用）リサイクル（再生）の究極の姿がゼロエミッションだ。
原材料、エネルギーをいただいたら、返礼すべきだ。自分ばかりが儲かることを考えてはいけない。地球環境に「礼尚往来」の礼を尽くさねば、企業は市場から淘汰されることになる。

環境にやさしくコストダウン

原材料・エネルギーを節約するのが、リデュース。使えるモノを捨てないで再利用するのがリユース。使えなくなったものを再生利用するのがリサイクルだ。これらを活用して、静脈をしっかり持たなければならない。
資源を使わせていただくことに感謝し、リデュース・リユースをすればコストダウンにもなる。リサイクルにはコストがかかるが、トータルで考えればコストダウンになる。
例えば発泡スチロールの梱包材を再生する小型プラントを、工場や倉庫に持つ。かさばる梱包材を運搬せず、原材料の形で運搬すれば輸送費が節約でき、その分の二酸化炭素排出も削減できるはずだ。

究極のゼロエミッション

　究極のゼロエミッションは、生産に投入した原材料は全て使い切り、廃棄物をゼロにすることだ。
例えば従業員食堂で発生した残飯もリサイクルする。残飯から堆肥を作り、その堆肥で再び食材を育てる。食の安全が懸念されている今、無農薬・有機肥料で栽培した食材を使えば、従業員の健康にも貢献できる。
実はこの方面も日本の環境技術は大変優れている。小さな堆肥プラントを導入すれば、工場内で完結するゼロエミッションが実現可能だ。
堆肥プラントを併設した農場を消費地の近郊に作る。都市型農園だ。この様な環境調和型のビジネスが盛んになれば、中国の食の安全問題は、大幅に改善できるのではないだろうか？
早いもので、この連載を初めて1年が経った。12回のコラムにお付き合いいただいた読者の皆様に感謝したい。
すでにお気づきの読者様もおありかも知れないが、毎回ご紹介した四文字熟語は中文読みで尻取りになっている。ぜひバックナンバーをご確認いただきたい。
ではまたどこかでお目にかかりましょう。

本コラムは香港，中国華南地区で発行されている月刊ビジネス雑誌「華南マンスリー」2010年5月号に寄稿したコラムです．

原田指導語録

このブログでしばしばご紹介している「伝説の経営者」「奇跡の工場再建屋」原田則夫氏の経営哲学の根底には，人のココロを理解し，成長を願い教育・指導するということである．言われてみれば当たり前のことであり，日本が戦後急成長した背景には，人を育て活用するという考え方があったはずだ．
しかし20世紀末から日本は自信を失い，日本企業が元来持っていたはずの「人を育てて使う」という強みが忘れ去られたように感じている．安易に現場を派遣職員に置き換え，経費を変動費化し経営の数字だけつじつまを合わせる．景気が悪くなると「派遣切り」が社会問題となる．人を大切にする日本的経営が失われつつある．
そんな風潮の中，原田氏の教えをもう一度研究しなおす必要がある．私の手元にあるのは「原田則夫指導語録」だ．原田氏の元秘書が二代に渡って，原田氏の現場指導を記録したものだ．
原田氏が日々どのような話題を捕らえ，どのように中国人部下を指導していたかよく分かる．
日本人経営者，経営幹部ばかりではなく，中国人経営幹部・リーダにもぜひ読んで欲しい．この「原田指導語録」をテキストとして，社内で研修会をすれば効果が上がるだろう．
コンサルタントとして社内研修なども仕事にしているが，本当のことを言うと自社で研修をしたほうが効果は高いはずだ．



こちらの記事もどうぞ
原田式マネジメント14か条

【統計的品質管理】pn管理図

二項分布に従う計数値で，統計的品質管理（SQC）・統計的工程管理（SPC）をするためのpn管理図の作成方法を紹介します．

pn管理図の作り方

毎ロット同じ数だけ生産する場合に使います．
pはロットの不良率，nは検査台数です．
従ってpnは不良の個数です．
不良の個数（pn）は二項分布に従います．
不良台数は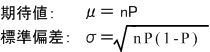，pn管理図

P：工程の不良発生率の実力値．

つまり毎ロット発生する不良個数は，μを平均とし標準偏差σでばらつくということになります．
小文字pで表記する場合は，不良率がPの実力を持つ工程で生産した場合の，毎ロットの不良率の観測値ということになります．
ここで
nP≧5と(1-nP)≧5が成り立つ場合は，二項分布を正規分布に近似しても実用上問題ありません．
例えば，検査工程で0.5％の不良が発生する場合1ロットの大きさが1000個であればnP＝5，n(1-P)＝995となり両者とも5以上なので，正規分布に近似出来ます．
つまり不良個数が平均±3σの中に入る確率は99.7％であり，正常と判断する．
不良個数が平均値±3σを外れた場合は，工程に何か異常があったと判断する．
という計量値の統計的品質管理と同じ考え方です．

【手順1】
ロットのサイズnが同じ検査データを20組以上取り，不良個数pnを調べる．
検査データは実力（不良発生率）が同じと判断できるデータでなければなりません．
また実力が同じと判断できても，違うラインの不良個数を一つの管理図で管理するのは，管理の趣旨から外れます．

【手順2】
平均不良個数，平均不良率を求める．
不良率

pn：ロットの不良数
k：ロットの数
n：ロットの大きさ

【手順3】
pn管理図の上側管理限界（UCL*1），下側管理限界（LCL*2）を求める．

*1UCL：Upper Control Limit　上側管理限界
*2LCL：Lower Control Limit　下側管理限界

上限・下限管理線

【手順4】
pn管理図を作り，エックスバーチャートと同じように毎ロットデータを記入する．
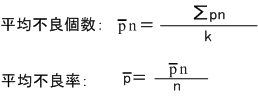
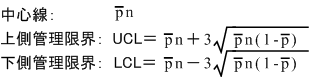
photo_5

【手順5】
pn管理図の変動をモニターして，問題があれば原因を究明して処置・対策をする．
判定方法はエックスバー・アール管理図の判定方法を参照下さい．

ところでpn管理図に下側管理限界（LCL）があるのに違和感をもたれる方があるかも知れません．不良が少なければ少ない方が良いわけだから，下側管理限界に意味があるのかという質問を受けることがあります．
統計確率理論の考え方では，毎ロットの不良率は一定の幅の中にばらついている，という考え方をします．従って工程改善などにより，実力値（不良率P）が変わっていなければ，下側管理限界（LCL）を割ることは無い．もし下側管理限界（LCL）を割った場合は，検査に不備があり不良品を良品として判定してしまったと，考えるのが合理的です．