計量値(重さ,長さ,電圧,電流など量として測定できるモノ)の平均値(xbar・エックスバー)と範囲(R・アール)が「偶然要因」によるばらつきの範囲内に入っているかどうかを確認するための管理図である.
ロットからサンプルを取り,サンプルの平均値をロット全体の平均値の推定値,範囲(サンプルの最大値-最小値)をロット全体のばらつきの推定値として考える.
この平均値と範囲が工程能力のばらつき(±3σ)の範囲内にあれば管理状態にあると考える.従って管理図の上下限の管理限界に引かれる線は,検査仕様の上下限ではない.1000個モノを作ったら997個まではこの範囲に入るだろうと言う実力値の上下限線である.
通常は検査仕様のほうが工程能力のばらつきより幅が広いので,製品が不合格になる前に「異常要因」が発生していることに気が付く事が出来るわけである.
では具体的にxbar-R(エックスバーアール)管理図の作り方を解説しよう.
例えば同じ加工機械で加工した製品の仕上がり寸法を2時間おきに抜き取り検査をした値などが利用できる.すなわち時系列に抜き取りサンプル数だけのデータの群ができる.
データは100個以上ある事が望ましい.
群の大きさ(ロットごとの抜き取りサンプル数)は大きければ精度が上がるが検査工数がかかる,小さければ検査工数は小さいが精度が落ちると言うことになる.通常はn=2~5程度で考えれば良い.
(私はn=5,6程度でサンプリングする事が多い)
このデータがこの工程の工程能力をあらわしていると考える.
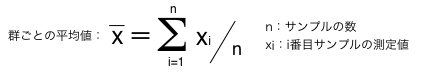
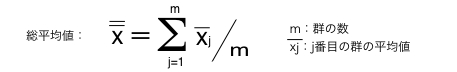
総平均(平均値の平均値)が平均値の中心値となる.
xbar(エックスバー)管理図中心線
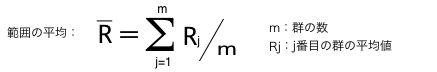
範囲の平均値が範囲の中心値になる.
R(アール)管理図中心線
xbar(エックスバー)管理図上限・下限管理限界
R(アール)管理図上限・下限管理限界
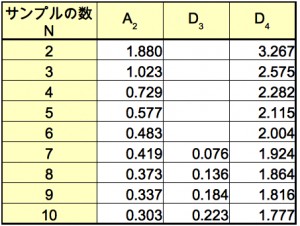
それぞれの係数A2,D3,D4は管理図用係数表による.D3が空欄の場合は,下限管理線を設定しない.
中心線(実践)と上下の管理限界線(点線)を入れる.(図には管理限界線を赤色線,中心線を黄色線で示した)
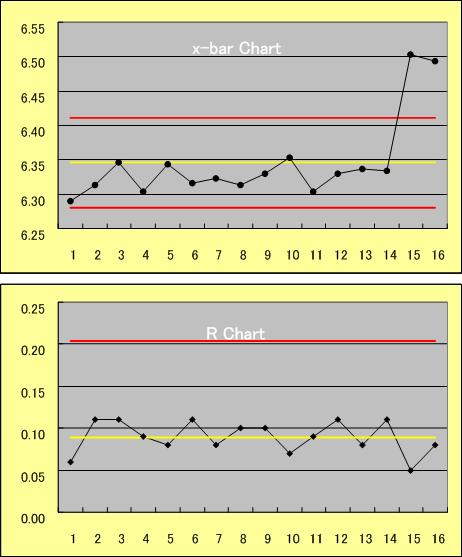
このような手順で作成したxbar-R(エックスバーアール)管理図でロットごとにサンプルを5個程度抜き取り,平均値と範囲を計算して管理図にプロットを続ける.
この管理図により,工程で予期しない「異常要因」が発生したときにアラームが出るようになる.
異常と判断するのは工程能力のばらつき(±3σ)を外れたときなので,工程内検査で不良が発生する(検査規格を外れる)前に異常を検出できることになる.
工程管理図を書いて上限,下限を超えれば工程に異常が発生していると考えてよい.
上下限を超えていなくても異常と判断すべき場合がある.
詳しくはこちらの記事へ
